54. 螺旋矩阵
1. 题目
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例 1:
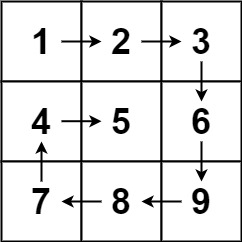
1 | 输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] |
示例 2:
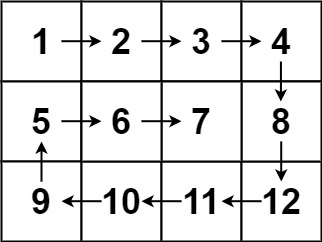
1 | 输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]] |
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 10-100 <= matrix[i][j] <= 100
2. 思路
- 已知题目需要顺时针转弯,因此需要有一个转弯的思路,怎么转弯并且保证转弯之后的方向持续不变直至下标越界或该值已读取
- 由上述思路首先衍生出2个小问题,一个是判断下标是正常下标,第二个是判断该值已经被读取
- 针对判断下标可结合
matrix二维数组得到行数与列数,从而进行下标合法性的判断 - 针对判断数值是否已读取过,可读取过后将该值设置为其他变量(如
Integer.MAX_VALUE),以表示该值已读取
- 针对判断下标可结合
- 要进行方向的扭转,可配合二维数组实现,首先可以通过官方图示知道螺旋矩阵读取一共会出现四个方向,分别是:右 -> 下 -> 左 -> 上
- 以上方向的转动无非是下标的转动,那么通过定义出代表方向的二维数组代表四个方向的下标移动方向
- 如
direction = {0, 1}代表向右移动1个单位,row + direction[0]即可得到下一个行坐标,column + direction[1]即可得到下一个列坐标 - 在出现下标越界或出现该值标记为已读取时,则进行转弯操作
- 因为转弯的方向会循环持续为: 右 -> 下 -> 左 -> 上 -> 右 -> 下 -> …,而代表方向的二维数组
DIRECTIONS只有四个子数值,因此代表方向的下标directionIndex将采取取余+1的方式来确保达到循环的效果- 即新的方向下标为:
directionIndex = (directionIndex + 1) % 4
- 即新的方向下标为:
3. 代码
1 | class Solution { |
4. 复杂度
- 时间复杂度:O(1)
- 空间复杂度:O(1)