52. N 皇后 II

1. 题目

n 皇后问题 研究的是如何将 n 个皇后放置在 n × n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回 n 皇后问题 不同的解决方案的数量。

示例 1：

img

1
2
3
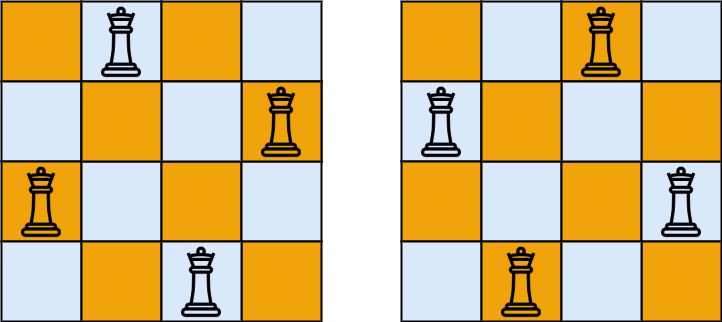
输入：n = 4
输出：2
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

1
2
输入：n = 1
输出：1

提示：

  • 1 <= n <= 9

2. 思路

  • N皇后的本质在于限制每一列 & 每一对角线（包含左对角线与右对角线）均只能够包含存在一颗棋子
  • 提前需要知道的是每一个方向对角线的数量为n * 2 - 1条，如下所示：

image-20240110110436192

  • 初始化列数组cols与左右对角线数组leftDiagonals, rightDiagonals，其中列数组的长度为n，左右对角线数组的长度为n * 2 - 1
  • 初始化回溯函数helper(int row)，回溯模板为以下：
1
2
3
4
5
6
7
8
9
10
11
12
void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}
  • 回溯函数中，终止条件为当row == n时，将全局result变量进行+1，同时终止回溯
  • 回溯过程中，入参单位为每一行的矩阵，深度回溯的过程中，使用的是每一列
  • 在判断该坐标允许放置棋子时，需要将列数组、左右对角线数组标记为占用状态
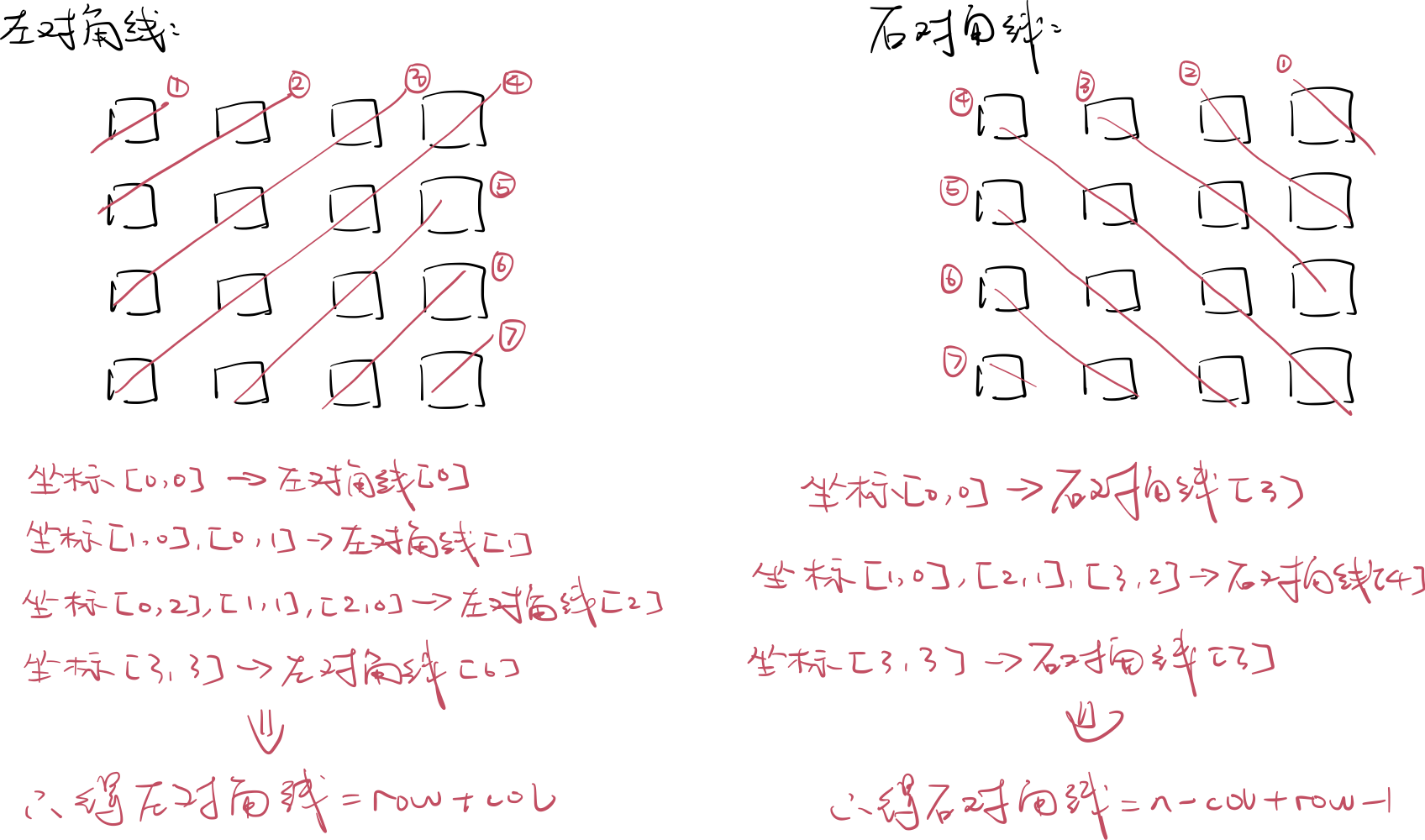
  • 其中左对角线的计算为row + col，右对角线的计算是n - col + row - 1，如下所示：

image-20240110114429949

  • 执行完回溯步骤后，需要将对应标记结果进行撤销

3. 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
class Solution {
    private int[] cols;
    private int[] leftDiagonals;
    private int[] rightDiagonals;
    private int n;
    private int result;

    public int totalNQueens(int n) {
        this.n = n;
        this.cols = new int[n];
        this.leftDiagonals = new int[n * 2 - 1];
        this.rightDiagonals = new int[n * 2 - 1];
        
        helper(0);
        
        return result;
    }

    private void helper(int row) {
        if (row == n) {
            result++;
            return;
        }

        for (var col = 0; col < n; ++col) {
            if (allowLocate(row, col)) {
                cols[col] = 1;
                leftDiagonals[row + col] = 1;
                rightDiagonals[n - col + row - 1] = 1;

                helper(row + 1);

                cols[col] = 0;
                leftDiagonals[row + col] = 0;
                rightDiagonals[n - col + row - 1] = 0;
            }
        }
    }

    private boolean allowLocate(int row, int col) {
        if (cols[col] == 1) {
            return false;
        }

        if (leftDiagonals[row + col] == 1) {
            return false;
        }

        if (rightDiagonals[n - col + row - 1] == 1) {
            return false;
        }

        return true;
    }
}

4. 复杂度

  • 时间复杂度：O(n!)
  • 空间复杂度：O(n)

image-20230821225503575