48. 旋转图像

1. 题目

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

img

1
2
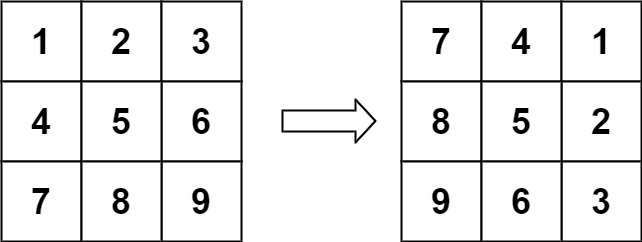
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

img

1
2
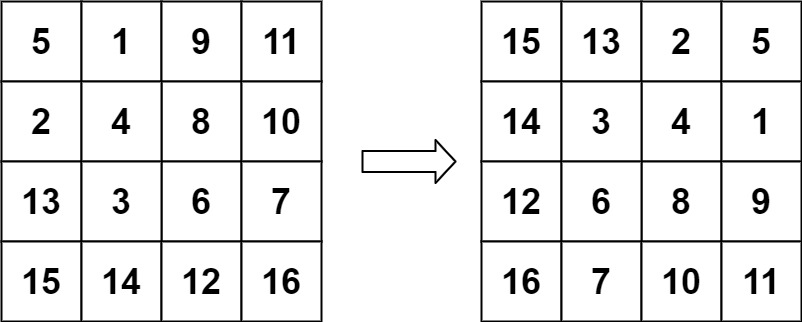
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示：

  • n == matrix.length == matrix[i].length
  • 1 <= n <= 20
  • -1000 <= matrix[i][j] <= 1000

2. 思路

  • 根据题目要求，已知需要将矩阵内的数值顺时针旋转90度后摆放，同时只能进行原地旋转
  • 通过观察，发现将矩阵沿着对称线进行交换，再次沿着中心线进行交换，即可得到最终旋转后的矩阵排列，如下图所示
  • 设计到原地交换矩阵内的数值，可采用位运算进行AB数值的交换，具体公式为：a = a ^ b ^ (b = a)

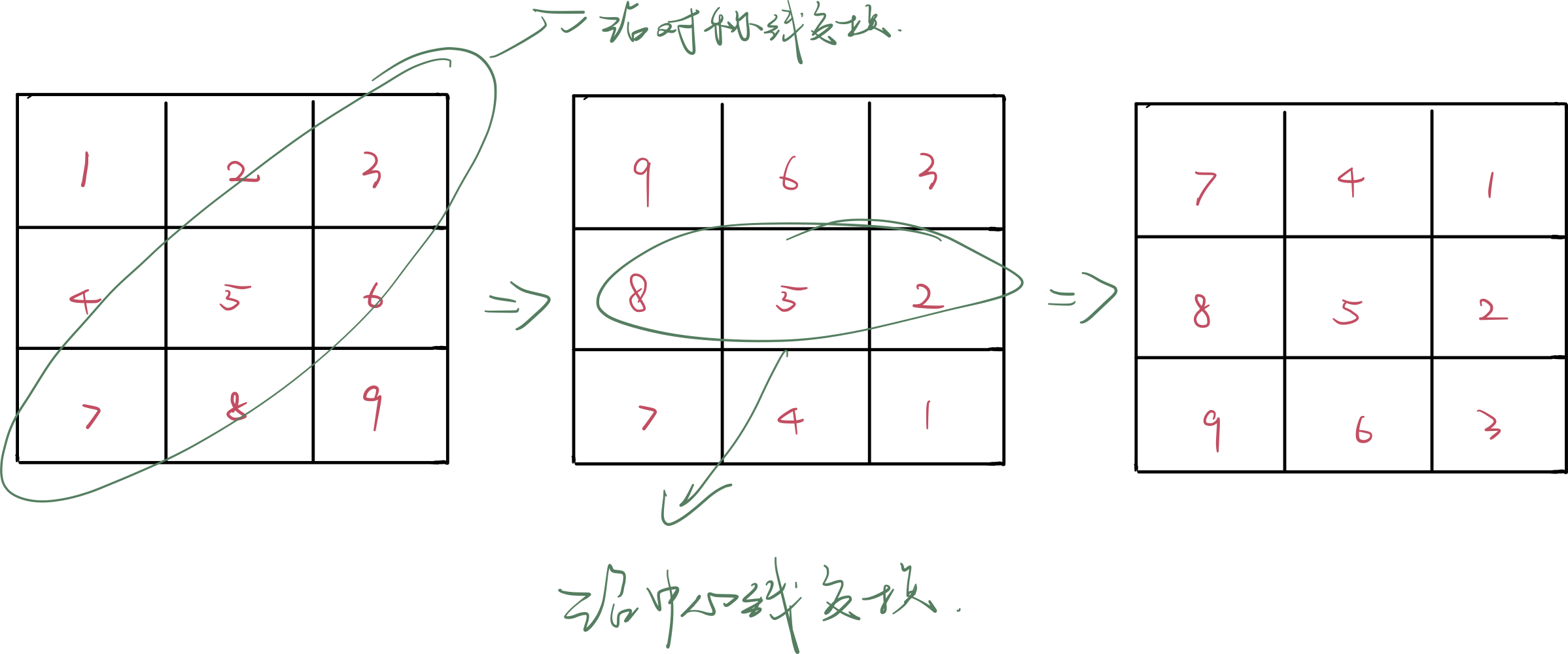
image-20230823005542535

  • 以上思路的代码实现过程当中，难点其实在于怎么把控进行交换的元素下标
  • 上图中的第一个矩阵需要沿着对称线进行对称交换，实际上需要操作的下标为[0, 0] -> [2, 2], [0, 1] -> [1, 2], [1, 0] -> [2, 1]，剩余的下标则无需再交换，因此可以发现规律为
    • 需要反转的行下标为reverseRow = rows - j - 1
    • 需要反转的列下标为reverseColumn = columns - i - 1
  • 上图中的第二个矩阵需要沿着中心线进行对称交换，实际上需要操作的下标为[0, 0] -> [2, 2], [0, 1] -> [2, 1], [0, 2] -> [2, 2]
    • 需要反转的行下标为reverseRow = rows - i - 1
    • 列下标无需变化
  • 由此得出以下实现代码

3. 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public void rotate(int[][] matrix) {
        var rows = matrix.length;
        var columns = matrix[0].length;

        for (var i = 0; i < rows; ++i) {
            for (var j = 0; j < columns - i - 1; ++j) {
                var reverseRow = rows - j - 1;
                var reverseColumn = columns - i - 1;
                matrix[i][j] = matrix[i][j] ^ matrix[reverseRow][reverseColumn] ^ (matrix[reverseRow][reverseColumn] = matrix[i][j]);
            }
        }

        for (var i = 0; i < rows / 2; ++i) {
            for (var j = 0; j < columns; ++j) {
                var reverseRow = rows - i - 1;
                matrix[i][j] = matrix[i][j] ^ matrix[reverseRow][j] ^ (matrix[reverseRow][j] = matrix[i][j]);
            }
        }
    }
}

4. 复杂度

  • 时间复杂度：O(1)
  • 空间复杂度：O(1)

image-20230823005517027