399. 除法求值

1. 题目

给你一个变量对数组 equations 和一个实数值数组 values 作为已知条件，其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。

另有一些以数组 queries 表示的问题，其中 queries[j] = [Cj, Dj] 表示第 j 个问题，请你根据已知条件找出 Cj / Dj = ? 的结果作为答案。

返回 所有问题的答案 。如果存在某个无法确定的答案，则用 -1.0 替代这个答案。如果问题中出现了给定的已知条件中没有出现的字符串，也需要用 -1.0 替代这个答案。

注意：输入总是有效的。你可以假设除法运算中不会出现除数为 0 的情况，且不存在任何矛盾的结果。

注意：未在等式列表中出现的变量是未定义的，因此无法确定它们的答案。

示例 1：

1
2
3
4
5
6
7
输入：equations = [["a","b"],["b","c"]], values = [2.0,3.0], queries = [["a","c"],["b","a"],["a","e"],["a","a"],["x","x"]]
输出：[6.00000,0.50000,-1.00000,1.00000,-1.00000]
解释：
条件：a / b = 2.0, b / c = 3.0
问题：a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ?
结果：[6.0, 0.5, -1.0, 1.0, -1.0 ]
注意：x 是未定义的 => -1.0

示例 2：

1
2
输入：equations = [["a","b"],["b","c"],["bc","cd"]], values = [1.5,2.5,5.0], queries = [["a","c"],["c","b"],["bc","cd"],["cd","bc"]]
输出：[3.75000,0.40000,5.00000,0.20000]

示例 3：

1
2
输入：equations = [["a","b"]], values = [0.5], queries = [["a","b"],["b","a"],["a","c"],["x","y"]]
输出：[0.50000,2.00000,-1.00000,-1.00000]

提示：

  • 1 <= equations.length <= 20
  • equations[i].length == 2
  • 1 <= Ai.length, Bi.length <= 5
  • values.length == equations.length
  • 0.0 < values[i] <= 20.0
  • 1 <= queries.length <= 20
  • queries[i].length == 2
  • 1 <= Cj.length, Dj.length <= 5
  • Ai, Bi, Cj, Dj 由小写英文字母与数字组成

2. 思路

  • 并查集（不相交集合）用于处理动态连通性问题，其中一个应用就是求解「最小生成树」的Kruskal算法
  • 并查集支持查询（find）和合并（union）两个关键的操作，同时它只回答两个节点是否在同一个连通分量重，并不回答路径问题
  • 并差集的常见设计思想是把同一个连通分量重的节点组织成一个树形结构
  • 已知题目要求按照已知的连通权重计算出不同节点之间的值，而将不同变量转化为相同变量的倍数，进行标准统一，则可解决不同节点之间计算值的问题
  • 如已知a / b = 2.0, b / c = 3.0，则可对应转化为a / c = 2b / c = 6.0，对应b / a = b / 2b = 1 / 2 = 0.5
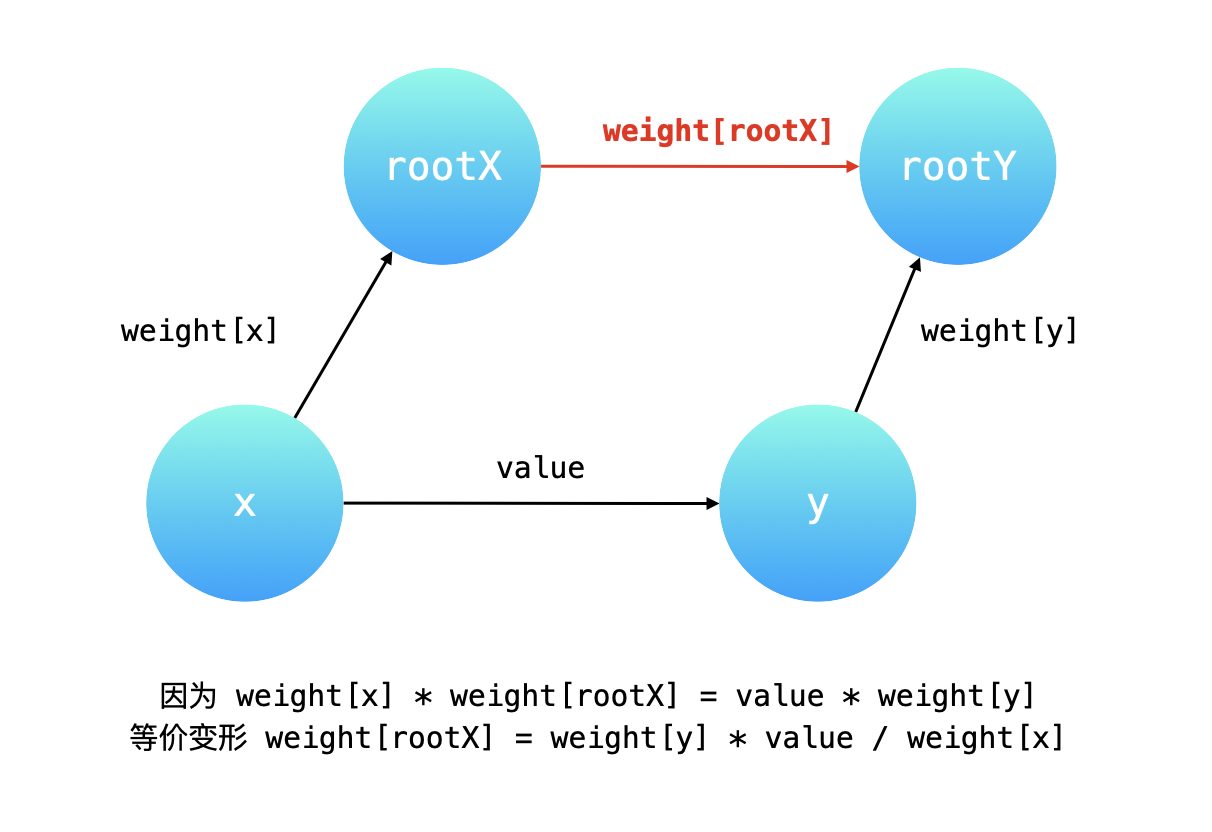
  • 因此根据已知，可以将题目给出的信息比如a -(2.0)-> b -(3.0)-> c对应转化为 a -(6.0)-> c <-(3.0)- b
  • 对应使用并查集的过程中，字母采用整数型ID代表，同时初始化权重量weights来表示系数，同时在遍历的过程中，将每一组连通量进行union操作，如下所示：

image.png

  • 完成所有边的合并后，通过并查集查找find来确认是否能够获取对应queries数组的除法求值，如果无法获取到，则直接返回-1.0结果
  • 两个节点是否连通意味着是否能够有标准的变量统一可以进行计算，如果连通（通过节点的parent判断父节点是否一致可以判断连通性），则可直接进行queries除法求值

3. 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
class Solution {
    public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {
        var size = equations.size() * 2;
        var unionFind = new UnionFind(size);
        var map = new HashMap<String, Integer>(size);
        var result = new double[queries.size()];

        var id = 0;
        for (var i = 0; i < equations.size(); ++i) {
            var equation = equations.get(i);
            var parameterX = equation.get(0);
            var parameterY = equation.get(1);

            if (!map.containsKey(parameterX)) {
                map.put(parameterX, id);
                id++;
            }

            if (!map.containsKey(parameterY)) {
                map.put(parameterY, id);
                id++;
            }

            unionFind.union(map.get(parameterX), map.get(parameterY), values[i]);
        }

        for (var i = 0; i < queries.size(); ++i) {
            var query = queries.get(i);
            var queryParameterX = query.get(0);
            var queryParameterY = query.get(1);

            if (!map.containsKey(queryParameterX) || !map.containsKey(queryParameterY)) {
                result[i] = -1.0d;
            } else {
                result[i] = unionFind.isConnected(map.get(queryParameterX), map.get(queryParameterY));
            }
        }

        return result;
    }

    class UnionFind {
        private int[] parent;
        private double[] weights;

        public UnionFind(int size) {
            this.parent = new int[size];
            this.weights = new double[size];

            for (var i = 0; i < size; ++i) {
                parent[i] = i;
                weights[i] = 1.0d;
            }
        }

        
        public void union(int x, int y, double value) {
            var xRoot = find(x);
            var yRoot = find(y);

            if (xRoot == yRoot) {
                return;
            }

            parent[xRoot] = yRoot;
            weights[xRoot] = weights[y] * value / weights[x];
        }

        public int find(int x) {
            if (parent[x] != x) {
                var originParent = parent[x];
                parent[x] = find(parent[x]);
                weights[x] *= weights[originParent];
            }
            return parent[x];
        }

        public double isConnected(int x, int y) {
            var xRoot = find(x);
            var yRoot = find(y);

            if (xRoot == yRoot) {
                return weights[x] / weights[y];
            }

            return -1.0d;
        }
    }
}

4. 复杂度

  • 时间复杂度: O((N+Q)logA)

    • 构建并查集 O(Nlog⁡A) ，这里 N 为输入方程 equations 的长度，每一次执行合并操作的时间复杂度是 O(log⁡A)，这里 A 是 equations 里不同字符的个数
    • 查询并查集 O(Qlog⁡A)，这里 Q 为查询数组 queries 的长度，每一次查询时执行「路径压缩」的时间复杂度是 O(log⁡A)

  • 空间复杂度: O(n)

image-20231122214737750