36. 有效的数独

1. 题目

请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ，验证已经填入的数字是否有效即可。

  1. 数字 1-9 在每一行只能出现一次。
  2. 数字 1-9 在每一列只能出现一次。
  3. 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

注意：

  • 一个有效的数独（部分已被填充）不一定是可解的。
  • 只需要根据以上规则，验证已经填入的数字是否有效即可。
  • 空白格用 '.' 表示。

示例 1：

img

1
2
3
4
5
6
7
8
9
10
11
输入：board = 
[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出：true

示例 2：

1
2
3
4
5
6
7
8
9
10
11
12
输入：board = 
[["8","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出：false
解释：除了第一行的第一个数字从 5 改为 8 以外，空格内其他数字均与 示例1 相同。 但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。

提示：

  • board.length == 9
  • board[i].length == 9
  • board[i][j] 是一位数字（1-9）或者 '.'

2. 思路

  • 本质上需要对行和列以及9*9的小矩阵进行检验，因此整体思路按照3条规则划分成3个方法
  • 对行和对列进行查重采用的是传统的暴力手段配合着哈希表完成
  • 对小矩阵的查重判断比较费心思，需要按矩阵进行检查，因此首先对矩阵按照0-8进行排号，根据矩阵好计算出初始单元格坐标和结束单元格坐标，每个小矩阵的行和列步增最多都为2，再配合哈希表进行去重，按照矩阵进行编号如下所示：

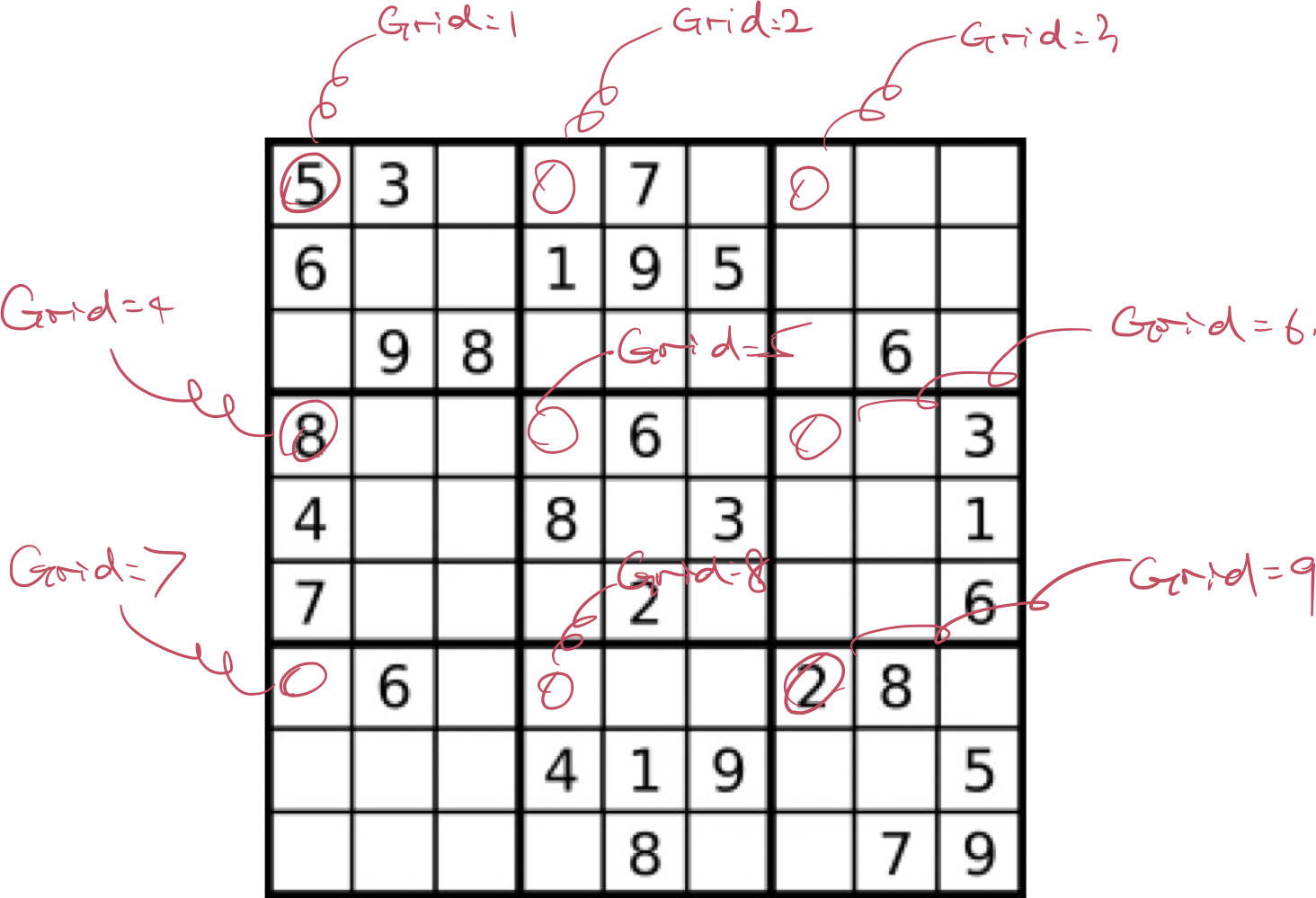
image-20230820150833977

  • 小矩阵起始坐标计算公式为：
    • 行：(矩阵号 / 3) * 3
    • 列：(矩阵号 % 3) * 3

3. 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
class Solution {
    private static final char NULL_VALUE = '.';

    public boolean isValidSudoku(char[][] board) {
        return checkEveryRow(board) && checkEveryColumn(board) && checkEveryGrid(board);
    }

    private boolean checkEveryRow(char[][] board) {
        for (var i = 0; i < 9; ++i) {
            var map = new int[9];
            for (var j = 0; j < 9; ++j) {
                if (board[i][j] != NULL_VALUE) {
                    var index = board[i][j] - '1';
                    if (map[index] >= 1) {
                        return false;
                    }
                    map[index]++;
                }
            }
        }
        return true;
    }

    private boolean checkEveryColumn(char[][] board) {
        for (var i = 0; i < 9; ++i) {
            var map = new int[9];
            for (var j = 0; j < 9; ++j) {
                if (board[j][i] != NULL_VALUE) {
                    var index = board[j][i] - '1';
                    if (map[index] >= 1) {
                        return false;
                    }
                    map[index]++;
                }
            }
        }
        return true;
    }

    private boolean checkEveryGrid(char[][] board) {
        for (var i = 0; i < 9; ++i) {
           if (!checkGrid(board, i)) {
               return false;
           }
        }
        return true;
    }

    private boolean checkGrid(char[][] board, int index) {
        var startColumn = (index % 3) * 3;
        var startRow = (index / 3) * 3;
        var endColumn = startColumn + 2;
        var endRow = startRow + 2;
        var map = new int[9];

        for (var i = startRow; i <= endRow; ++i) {
            for (var j = startColumn; j <= endColumn; ++j) {
                if (board[i][j] != NULL_VALUE) {
                    var mapIndex = board[i][j] - '1';
                    if (map[mapIndex] >= 1) {
                        return false;
                    }
                    map[mapIndex]++;
                }
            }
        }
        return true;
    }
}

4. 复杂度

  • 时间复杂度：O(1)
  • 空间复杂度：O(1)

image-20230820150446072