212. 单词搜索 II

1. 题目

给定一个 m x n 二维字符网格 board 和一个单词（字符串）列表 words， 返回所有二维网格上的单词 。

单词必须按照字母顺序，通过 相邻的单元格 内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母在一个单词中不允许被重复使用。

示例 1：

img

1
2
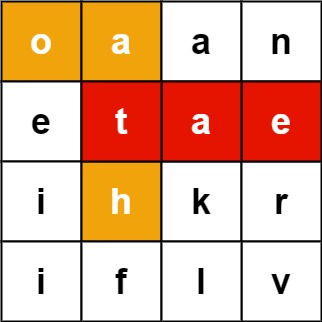
输入：board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
输出：["eat","oath"]

示例 2：

img

1
2
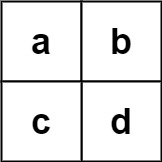
输入：board = [["a","b"],["c","d"]], words = ["abcb"]
输出：[]

提示：

  • m == board.length
  • n == board[i].length
  • 1 <= m, n <= 12
  • board[i][j] 是一个小写英文字母
  • 1 <= words.length <= 3 * 10^4
  • 1 <= words[i].length <= 10
  • words[i] 由小写英文字母组成
  • words 中的所有字符串互不相同

2. 思路

  • 已知题目要求获取的是board内所有能够组成words内任意一个单词的单词集合，也就是说，要获取的是在board二维数组中，能够找到任意一个单词序列（可以拐弯）存在于words单词列表中的字符串集合
  • 整体思路可以将words转化为前缀树，在回溯二维数组board进行字符串存在判断，如果存在，则记录在结果集中，有关前缀树的实现，可以参考208. 实现Tire(前缀树)进行复习，不同的是需要在Tire节点中加入word变量用于后续的取值，word变量则是当前节点为最终节点时，将当前匹配的字符串赋值给Tire节点中的word变量
  • 根据题目提示，可以知道word[i]中均由小写字母构成，因此前缀树节点Tire的children即可初始化为长度为26的数组
  • 第一步则是将方法参数的words单词列表统一转化为前缀树
  • 第二步则是根据前述的前缀树转化，对board二维数组进行逐一回溯判断，根据题目要求同一个单元格内的字母在一个单词中不允许被重复使用，因此将在回溯前将对应的单元格加上访问标记，在回溯后去除对应的访问标记（此处利用的是visitRecord）
  • 回溯的过程中，如果遇到当前Tire节点为最终节点，则直接获取Tire类中的word元素，将其添加至结果字符串集合中，同时为了防止重复添加，需要将最终节点标识标记为false，相当于前缀树的删除操作，此处需要注意的是，当遇到了最终节点，添加到结果集合中后，仍需继续进行深度遍历，因为有可能存在更长的匹配字符串

3. 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
class Solution {
    private static final int[][] DIRECTION = {{-1, 0}, {0, -1}, {1, 0}, {0, 1}};

    class Tire {
        String word;
        Tire[] children = new Tire[26];
        boolean isFinal = false;
    }

    private Tire root = new Tire();
    private int row;
    private int col;
    private boolean[][] visitRecord;
    private List<String> result = new ArrayList<>();

    public List<String> findWords(char[][] board, String[] words) {
        this.row = board.length;
        this.col = board[0].length;
        this.visitRecord = new boolean[row][col];
        
        for (var word : words) {
            insert(word);
        }

        for (var i = 0; i < row; ++i) {
            for (var j = 0; j < col; ++j) {
                var idx = board[i][j] - 'a';

                if (root.children[idx] != null) {
                    visitRecord[i][j] = true;
                    dfs(board, i, j, root.children[idx]);
                    visitRecord[i][j] = false;
                }
            }
        }

        return result;
    }

    private void dfs(char[][] board, int i, int j, Tire node) {
        if (node.isFinal) {
            this.result.add(node.word);
            node.isFinal = false;
        }

        for (var index = 0; index < DIRECTION.length; ++index) {
            var nextRow = i + DIRECTION[index][0];
            var nextCol = j + DIRECTION[index][1];
            var isValid = nextCol >= 0 && nextCol < col && nextRow >= 0 && nextRow < row;

            if (isValid && visitRecord[nextRow][nextCol] == false) {
                var nodeHashIndex = board[nextRow][nextCol] - 'a';

                if (node.children[nodeHashIndex] != null) {
                    visitRecord[nextRow][nextCol] = true;
                    dfs(board, nextRow, nextCol, node.children[nodeHashIndex]);
                    visitRecord[nextRow][nextCol] = false;
                }
            }
        }
    }

    private void insert(String word) {
        var arr = word.toCharArray();
        
        var node = root;
        for (var i = 0; i < arr.length; ++i) {
            var ch = arr[i];
            var idx = ch - 'a';

            var nextNode = node.children[idx];

            if (nextNode == null) {
                nextNode = new Tire();
            }

            node.children[idx] = nextNode;
            node = node.children[idx];
        }
        node.word = word;
        node.isFinal = true;
    }
}

4. 复杂度

  • 时间复杂度: 二维数组共有m * n个起点，每次能往4个方向搜索，且搜索的长度不会超过10，因此整体的时间复杂度则是O(m * n * 4^10)

  • 空间复杂度:
    $$
    O(\sum_{i=1}^{words.length - 1} word[i].length * C)，其中C为字符集的大小，本题的字符集大小固定为26
    $$

image-20231211235007909