135. 分发糖果

1. 题目

n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。

你需要按照以下要求，给这些孩子分发糖果：

  • 每个孩子至少分配到 1 个糖果。
  • 相邻两个孩子评分更高的孩子会获得更多的糖果。

请你给每个孩子分发糖果，计算并返回需要准备的 最少糖果数目 。

示例 1：

1
2
3
输入：ratings = [1,0,2]
输出：5
解释：你可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果。

示例 2：

1
2
3
4
输入：ratings = [1,2,2]
输出：4
解释：你可以分别给第一个、第二个、第三个孩子分发 1、2、1 颗糖果。
     第三个孩子只得到 1 颗糖果，这满足题面中的两个条件。

提示：

  • n == ratings.length
  • 1 <= n <= 2 * 104
  • 0 <= ratings[i] <= 2 * 104

2. 思路

  • 首先设立两个数组，分别为L和R，这两个数组的含义和生成规则分别为以下：

    • L数组：代表的是从左到右遍历ratings应当分配的糖果数量

      • 当ratings[i] > ratings[i - 1]时， L[i] = L[i - 1] + 1，这里是为了应对相邻两个孩子评分更高的孩子会获得更多的糖果的题目要求
      • 当ratings[i] < ratings[i - 1]时，L[i] = 1，这里是为了应对每个孩子至少分配到1个糖果的题目要求

    • R数组：代表的是从右到左遍历ratings应当分配的糖果数量

      • 当ratings[i] > ratings[i + 1]时，R[i] = R[i + 1] + 1，如上所述，为了应对相邻两个孩子评分更高的孩子会获得更多的糖果的题目要求
      • 当ratings[i] < ratings[i + 1]时，R[i] = 1，为了应对每个孩子至少分配到1个糖果的题目要求

  • 当计算出L数组和R数组后， 再次遍历同时采用变量count逐步累加计算Math.max(L[i], R[i])值，累加两个数组之间的最大值是因为左右规则都满足的情况下，小的值可能会破坏题目规则，而大的值可能不会破坏题目规则，比如：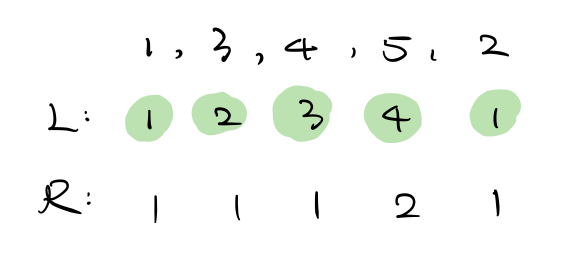

    分糖果-例子

    • 有且仅有当取L[i]和R[i]两者的最大值时，才能得到最少需要分配的糖果数量

Tips: 这里补充一个疑问点就是为什么一定需要R数组，根据一个简单的例子[1,2,3,2,1]，生成的L数组为[1,2,3,1,1]，如果没有R数组，则会导致下标3分配的糖果数量为1，此处不满足题目的第二个要求

3. 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int candy(int[] ratings) {
        var l = new int[ratings.length];
        var r = new int[ratings.length];
        var count = 0;
        l[0] = 1;
        for (var i = 1; i < ratings.length; ++i) {
            l[i] = (ratings[i - 1] < ratings[i]) ? l[i - 1] + 1 : 1;
        }

        r[ratings.length - 1] = 1;
        for (var i = ratings.length - 2; i >= 0; --i) {
            r[i] = (ratings[i + 1] < ratings[i]) ? r[i + 1] + 1 : 1;
        }

        for (var i = 0; i < ratings.length; ++i) {
            count += Math.max(l[i], r[i]);
        }

        return count;
    }
}

4. 复杂度

  • 时间复杂度: O(n)
  • 空间复杂度: O(n)

提交结果