129. 求根节点到叶节点数字之和

1. 题目

给你一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。

每条从根节点到叶节点的路径都代表一个数字：

  • 例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。

计算从根节点到叶节点生成的 所有数字之和 。

叶节点 是指没有子节点的节点。

示例 1：

img

1
2
3
4
5
6
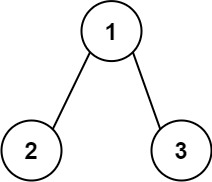
输入：root = [1,2,3]
输出：25
解释：
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此，数字总和 = 12 + 13 = 25

示例 2：

img

1
2
3
4
5
6
7
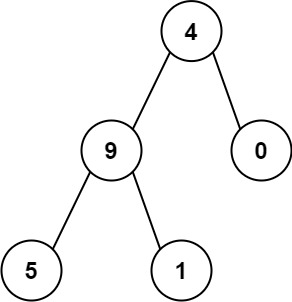
输入：root = [4,9,0,5,1]
输出：1026
解释：
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此，数字总和 = 495 + 491 + 40 = 1026

提示：

  • 树中节点的数目在范围 [1, 1000] 内
  • 0 <= Node.val <= 9
  • 树的深度不超过 10

2. 思路

  • 已知题目要求二叉树根节点到叶子节点的数字之和，意思是在非叶子节点时，仅对值进行val * 10 + node.val
  • 直到叶子节点时，才会将值与总值进行相加
  • 新建helper函数，入参是节点root和初始值val，当root为null时，返回的值为0
  • 过程中，将val值更新为val * 10 + root.val，并且当root为叶子节点时，返回val
  • 如果当前节点非叶子节点，则返回递归调用helper(root.left, val) + helper(root.right, val)的值

3. 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int sumNumbers(TreeNode root) {
        return helper(root, 0);
    }

    private int helper(TreeNode root, int val) {
        if (root == null) {
            return 0;
        }

        val *= 10;
        val += root.val;

        if (root.left == null && root.right == null) {
            return val;
        }

        return helper(root.left, val) + helper(root.right, val);
    }
}

4. 复杂度

  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

image-20231019212542493